DATA STRUCTURE

data structure and algorithm

DATA STRUCTURES:
                                 Data Structures are the programmatic way of storing data so that data can be used efficiently. Almost every enterprise application uses various types of data structures in one or other way. This tutorial will give you great understanding on Data Structures concepts needed to understand the complexity of enterprise level applications and need of algorithms, data structures.

ALGORITHM:

Algorithm is a step by step procedure, which defines a set of instructions to be executed in certain order to get the desired output. Algorithms are generally created independent of underlying languages, i.e. an algorithm can be implemented in more than one programming language.

According to data structure, some important categories of algorithms −

• 1.Search − Algorithm to search an item in a data structure.
• 2.Sort − Algorithm to sort items in certain order
• 3.Insert − Algorithm to insert item in a data structure
• 4.Update − Algorithm to update an existing item in a data structure
• 5.Delete − Algorithm to delete an existing item from a data structure

Characteristics of an Algorithm

Not all procedures can be called an algorithm. An algorithm should have the below mentioned characteristics −

• 1.Unambiguous − Algorithm should be clear and unambiguous. Each of its steps (or phases), and their input/outputs should be clear and must lead to only one meaning.
• I.Input − An algorithm should have 0 or more well defined inputs.
• II.Output − An algorithm should have 1 or more well defined outputs, and should match the desired output.
• 2.Finiteness − Algorithms must terminate after a finite number of steps.
• 3.Feasibility − Should be feasible with the available resources.
• 4.Independent − An algorithm should have step-by-step directions which should be independent of any programming code.

How to write an algorithm?

There are no well-defined standards for writing algorithms. Rather, it is problem and resource dependent. Algorithms are never written to support a particular programming code.

As we know that all programming languages share basic code constructs like loops (do, for, while), flow-control (if-else) etc. These common constructscan be used to write an algorithm.

We write algorithms in step by step manner, but it is not always the case. Algorithm writing is a process and is executed after the problem domain is well-defined. That is, we should know the problem domain, for which we are designing a solution.

Example

Let's try to learn algorithm-writing by using an example.

Problem − Design an algorithm to add two numbers and display result.

step 1 − START
step 2 − declare three integers a, b & c
step 3 − define values of a & b
step 4 − add values of a & b
step 5 − store output of step 4 to c
step 6 − print c
step 7 − STOP

Now we take an example to add two numbers

step 1 − START ADD
step 2 − get values of a & b
step 3 − c = a + b
step 4 − display c
step 5 − STOP

Data Definition

Data Definition defines a particular data with following characteristics.

• Atomic − Definition should define a single concept
• Traceable − Definition should be be able to be mapped to some data element.
• Accurate − Definition should be unambiguous.
• Clear and Concise − Definition should be understandable.

Data Object

Data Object represents an object having a data.

Data Type

Data type is way to classify various types of data such as integer, string etc. which determines the values that can be used with the corresponding type of data, the type of operations that can be performed on the corresponding type of data. Data type of two types −

• Built-in Data Type
• Derived Data Type

Built-in Data Type

Those data types for which a language has built-in support are known as Built-in Data types. For example, most of the languages provides following built-in data types.

1. Integers
2. Boolean (true, false)
3. Floating (Decimal numbers)
4. Character and Strings

download pdf DATA STRUCTURE

Derived Data Type

Those data types which are implementation independent as they can be implemented in one or other way are known as derived data types. These data types are normally built by combination of primary or built-in data types and associated operations on them. For example −

1. List
2. Array
3. Stack
4. Queue

Basic Operations

The data in the data structures are processed by various operations. The particular data structure chosen largely depends on the frequency of the operation that needs to be performed on the data structure.

• 1.Traversing
• 2.Searching
• 3.Insertion
• 4.Deletion
• 5.Sorting
• 6.Merging

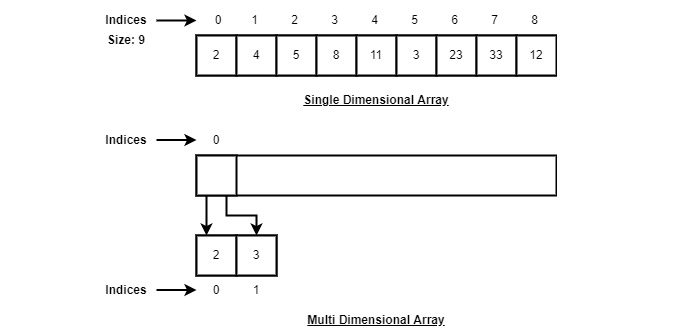
Array

Array is a container which can hold fix number of items and these items should be of same type. Most of the data structure make use of array to implement their algorithms. Following are important terms to understand the concepts of Array.

• Element − Each item stored in an array is called an element.
• Index − Each location of an element in an array has a numerical index which is used to identify the element.

Representation of An Array

Arrays can be declared in various ways in different languages. For illustration, let's take C array declaration.

Arrays can be declared in various ways in different languages. For illustration, let's take C array declaration.

following are the important points to be considered.

• Index starts with 0.
• Array length is 8 which means it can store 8 elements.
• Each element can be accessed via its index. For example, we can fetch element at index 6 as 9.
• Basic Operations

some basic operations of an array.

• 1. Traverse − print all the array elements one by one.
• 2. Insertion − add an element at given index.
• 3. Deletion − delete an element at given index.
• 4. Search − search an element using given index or by value.
• 5. Update − update an element at given index.

Insertion In Array

insert one or more data elements into an array. Based on the requirement, new element can be added at the beginning, end or any given index of array.

Here, we see a practical implementation of insertion operation, where we add data at the end of the array −

Algorithm

Let Array is a linear unordered array of MAX elements.

Example

Result

Let LA is a Linear Array (unordered) with N elements and K is a positive integer such that K<=N. Below is the algorithm where ITEM is inserted into the K^thposition of LA −

1. Start
2. Set J=N
3. Set N = N+1
4. Repeat steps 5 and 6 while J >= K
5. Set LA[J+1] = LA[J]
6. Set J = J-1
7. Set LA[K] = ITEM
8. Stop

Example

Below is the implementation of the above algorithm −

#include <stdio.h>
main() {
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;
   
   printf("The original array elements are :\n");
 
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   n = n + 1;
 
   while( j >= k){
      LA[j+1] = LA[j];
      j = j - 1;
   }
 
   LA[k] = item;
   
   printf("The array elements after insertion :\n");
 
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Result −

The original array elements are :
LA[0]=1 
LA[1]=3 
LA[2]=5 
LA[3]=7 
LA[4]=8 
The array elements after insertion :
LA[0]=1 
LA[1]=3 
LA[2]=5 
LA[3]=10 
LA[4]=7 
LA[5]=8 

Deletion In Array

Deletion refers to removing an existing element from the array and re-organizing all elements of an array.

Algorithm

Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Below is the algorithm to delete an element available at the K^thposition of LA.

1. Start
2. Set J=K
3. Repeat steps 4 and 5 while J < N
4. Set LA[J-1] = LA[J]
5. Set J = J+1
6. Set N = N-1
7. Stop

Example

#include <stdio.h>
main() {
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5;
   int i, j;
   
   printf("The original array elements are :\n");
 
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   j = k;
 
   while( j < n){
      LA[j-1] = LA[j];
      j = j + 1;
   }
 
   n = n -1;
   
   printf("The array elements after deletion :\n");
 
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Result −

The original array elements are :
LA[0]=1 
LA[1]=3 
LA[2]=5 
LA[3]=7 
LA[4]=8 
The array elements after deletion :
LA[0]=1 
LA[1]=3 
LA[2]=7 
LA[3]=8 

Searching In Array

You can perform a search for array element based on its value or its index.

Algorithm

Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Below is the algorithm to find an element with a value of ITEM using sequential search.

1. Start
2. Set J=0
3. Repeat steps 4 and 5 while J < N
4. IF LA[J] is equal ITEM THEN GOTO STEP 6
5. Set J = J +1
6. PRINT J, ITEM
7. Stop

Example

#include <stdio.h>
main() {
   int LA[] = {1,3,5,7,8};
   int item = 5, n = 5;
   int i = 0, j = 0;
   
   printf("The original array elements are :\n");
 
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   while( j < n){
 
      if( LA[j] == item ){
         break;
      }
  
      j = j + 1;
   }
 
   printf("Found element %d at position %d\n", item, j+1);
}

When compile and execute, above program produces the following result −

The original array elements are :
LA[0]=1 
LA[1]=3 
LA[2]=5 
LA[3]=7 
LA[4]=8 
Found element 5 at position 3

Update Operation

Update operation refers to updating an existing element from the array at a given index.

Algorithm

Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Below is the algorithm to update an element available at the K^thposition of LA.

1. Start
2. Set LA[K-1] = ITEM
3. Stop

Example

Below is the implementation of the above algorithm −

#include <stdio.h>
main() {
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5, item = 10;
   int i, j;
   
   printf("The original array elements are :\n");
 
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   LA[k-1] = item;

   printf("The array elements after updation :\n");
 
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

RESULT-

The original array elements are :
LA[0]=1 
LA[1]=3 
LA[2]=5 
LA[3]=7 
LA[4]=8 
The array elements after updation :
LA[0]=1 
LA[1]=3 
LA[2]=10 
LA[3]=7 
LA[4]=8 

 Linked List

A linked-list is a sequence of data structures which are connected together via links.

Linked List is a sequence of links which contains items. Each link contains a connection to another link. Linked list the second most used data structure after array. Following are important terms to understand the concepts of Linked List.

• Link − Each Link of a linked list can store a data called an element.
• Next − Each Link of a linked list contain a link to next link called Next.
• LinkedList − A LinkedList contains the connection link to the first Link called First.

• Linked List Representation

  Linked list can be visualized as a chain of nodes, where every node points to the next node.
  
  As per above shown illustration, following are the important points to be considered.
  • LinkedList contains an link element called first.
  • Each Link carries a data field(s) and a Link Field called next.
  • Each Link is linked with its next link using its next link.
  • Last Link carries a Link as null to mark the end of the list.

  Types of Linked List

  Following are the various flavours of linked list.
  • Simple Linked List − Item Navigation is forward only.
  • Doubly Linked List − Items can be navigated forward and backward way.
  • Circular Linked List − Last item contains link of the first element as next and and first element has link to last element as prev.

  Basic Operations

  Following are the basic operations supported by a list.
  • Insertion − add an element at the beginning of the list.
  • Deletion − delete an element at the beginning of the list.
  • Display − displaying complete list.
  • Search − search an element using given key.
  • Delete − delete an element using given key.

  Insertion Operation

  Adding a new node in linked list is a more than one step activity. We Shall learn this with diagrams here. First, create a node using the same structure and find the location where it has to be inserted.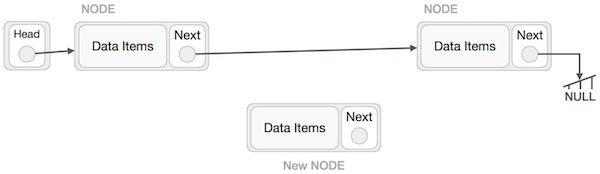
  
  Imagine that we are inserting a node B (NewNode), between A (LeftNode) and C (RightNode). Then point B.next to C

  NewNode.next −> RightNode;
  

  It should look like this −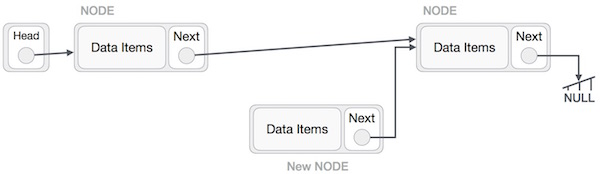
  
  Now the next of the node at left should point to the new node.

  LeftNode.next −> NewNode;
  

  
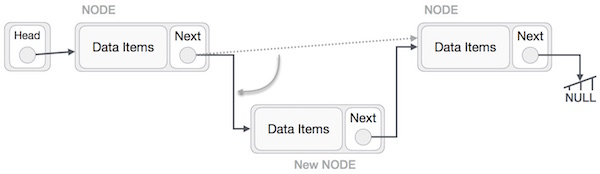  This will put the new node in the middle of the two. The new list should look like this −
  
  Similar steps should be taken if the node being inserted at the beginning of the list. While putting it at the end, then the second last node of list should point to new node and the new node will point to NULL.

  Deletion Operation

  Deletion is also a more than one step process. We shall learn with pictorial representation. First, locate the target node to be removed, by using searching algorithms.
  
  The left (previous) node of the target node now should point to the next node of the target node −

  LeftNode.next −> TargetNode.next;
  

  
  This will remove the link that was pointing to target node. Now we shall remove to what target node is pointing.

  TargetNode.next −> NULL;
  

  
  We need to use the deleted node we can keep that in memory otherwise we can simply deallocate memory and wipe off the target node completely.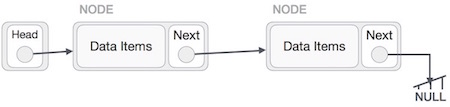
  

  Reverse Operation

  This operation is a thorough one. We need to make the last node be pointed by the head node and reverse the whole linked list.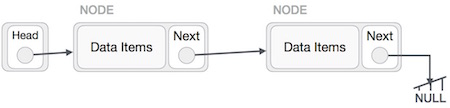
  
  First, we traverse to the end of the list. It should be pointing to NULL. Now we shall make it to point to its previous node −
  
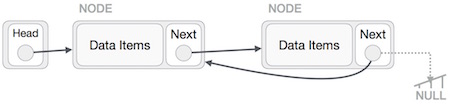  We have to make sure that last node is not the lost node, so we'll have some temp node, which looks like the head node pointing to the last node. Now we shall make our all our left side nodes to point to their previous nodes one by one.
  
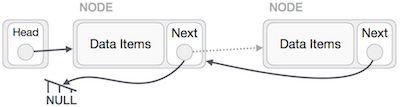  Except the node (first node) pointed by the head node, should point to their predecessor and making them their new successor. The first node will point to NULL.
  
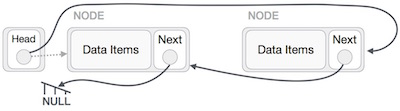  We'll make the head node to point the new first node by using temp node.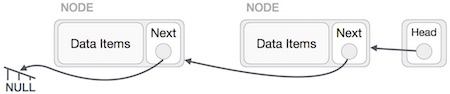
  
• A linked-list is a sequence of data structures which are connected together via links. Linked List is a sequence of links which contains items. Each link contains a connection to another link. Linked list the second most used data structure after array.

  Implementation in C

  #include <stdio.h>
  #include <string.h>
  #include <stdlib.h>
  #include <stdbool.h>
  
  struct node  
  {
     int data;
     int key;
     struct node *next;
  };
  
  struct node *head = NULL;
  struct node *current = NULL;
  
  //display the list
  void printList()
  {
     struct node *ptr = head;
     printf("\n[ ");
   
     //start from the beginning
     while(ptr != NULL)
   {        
        printf("(%d,%d) ",ptr->key,ptr->data);
        ptr = ptr->next;
     }
   
     printf(" ]");
  }
  
  //insert link at the first location
  void insertFirst(int key, int data)
  {
     //create a link
     struct node *link = (struct node*) malloc(sizeof(struct node));
   
     link->key = key;
     link->data = data;
   
     //point it to old first node
     link->next = head;
   
     //point first to new first node
     head = link;
  }
  
  //delete first item
  struct node* deleteFirst()
  {
  
     //save reference to first link
     struct node *tempLink = head;
   
     //mark next to first link as first 
     head = head->next;
   
     //return the deleted link
     return tempLink;
  }
  
  //is list empty
  bool isEmpty()
  {
     return head == NULL;
  }
  
  int length()
  {
     int length = 0;
     struct node *current;
   
     for(current = head; current != NULL; current = current->next)
   {
        length++;
     }
   
     return length;
  }
  
  //find a link with given key
  struct node* find(int key){
  
     //start from the first link
     struct node* current = head;
  
     //if list is empty
     if(head == NULL)
   {
        return NULL;
     }
  
     //navigate through list
     while(current->key != key){
   
        //if it is last node
        if(current->next == NULL){
           return NULL;
        }else {
           //go to next link
           current = current->next;
        }
     }      
   
     //if data found, return the current Link
     return current;
  }
  
  //delete a link with given key
  struct node* delete(int key){
  
     //start from the first link
     struct node* current = head;
     struct node* previous = NULL;
   
     //if list is empty
     if(head == NULL){
        return NULL;
     }
  
     //navigate through list
     while(current->key != key){
   
        //if it is last node
        if(current->next == NULL){
           return NULL;
        }else {
           //store reference to current link
           previous = current;
           //move to next link
           current = current->next;             
        }
    
     }
  
     //found a match, update the link
     if(current == head) {
        //change first to point to next link
        head = head->next;
     }else {
        //bypass the current link
        previous->next = current->next;
     }    
   
     return current;
  }
  
  void sort(){
  
     int i, j, k, tempKey, tempData ;
     struct node *current;
     struct node *next;
   
     int size = length();
     k = size ;
   
     for ( i = 0 ; i < size - 1 ; i++, k-- ) {
        current = head ;
        next = head->next ;
    
        for ( j = 1 ; j < k ; j++ ) {   
    
           if ( current->data > next->data ) {
              tempData = current->data ;
              current->data = next->data;
              next->data = tempData ;
  
              tempKey = current->key;
              current->key = next->key;
              next->key = tempKey;
           }
     
           current = current->next;
           next = next->next;                        
        }
     }   
  }
  
  void reverse(struct node** head_ref) {
     struct node* prev   = NULL;
     struct node* current = *head_ref;
     struct node* next;
   
     while (current != NULL) {
        next  = current->next;  
        current->next = prev;   
        prev = current;
        current = next;
     }
   
     *head_ref = prev;
  }
  
  main() {
  
     insertFirst(1,10);
     insertFirst(2,20);
     insertFirst(3,30);
     insertFirst(4,1);
     insertFirst(5,40);
     insertFirst(6,56); 
  
     printf("Original List: "); 
   
     //print list
     printList();
  
     while(!isEmpty()){            
        struct node *temp = deleteFirst();
        printf("\nDeleted value:");  
        printf("(%d,%d) ",temp->key,temp->data);        
     }  
   
     printf("\nList after deleting all items: ");          
     printList();
     insertFirst(1,10);
     insertFirst(2,20);
     insertFirst(3,30);
     insertFirst(4,1);
     insertFirst(5,40);
     insertFirst(6,56); 
     printf("\nRestored List: ");  
     printList();
     printf("\n");  
  
     struct node *foundLink = find(4);
   
     if(foundLink != NULL){
        printf("Element found: ");  
        printf("(%d,%d) ",foundLink->key,foundLink->data);  
        printf("\n");  
     }else {
        printf("Element not found.");  
     }
  
     delete(4);
     printf("List after deleting an item: ");  
     printList();
     printf("\n");
     foundLink = find(4);
   
     if(foundLink != NULL){
        printf("Element found: ");  
        printf("(%d,%d) ",foundLink->key,foundLink->data);  
        printf("\n");  
     }else {
        printf("Element not found.");  
     }
   
     printf("\n");  
     sort();
   
     printf("List after sorting the data: ");  
     printList();
   
     reverse(&head);
     printf("\nList after reversing the data: ");  
     printList();
  }

  If we compile and run the above program then it would produce following result −

  Output

  Original List: 
  [ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ]
  Deleted value:(6,56) 
  Deleted value:(5,40) 
  Deleted value:(4,1) 
  Deleted value:(3,30) 
  Deleted value:(2,20) 
  Deleted value:(1,10) 
  List after deleting all items: 
  [ ]
  Restored List: 
  [ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ]
  Element found: (4,1) 
  List after deleting an item: 
  [ (6,56) (5,40) (3,30) (2,20) (1,10) ]
  Element not found.
  List after sorting the data: 
  [ (1,10) (2,20) (3,30) (5,40) (6,56) ]
  List after reversing the data: 
  [ (6,56) (5,40) (3,30) (2,20) (1,10) ]

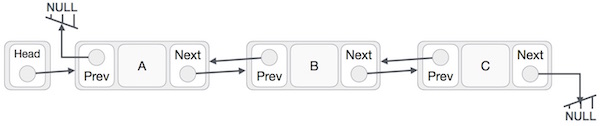
Doubly Linked List

Doubly Linked List is a variation of Linked list in which navigation is possible in both ways either forward and backward easily as compared to Single Linked List. Following are important terms to understand the concepts of doubly Linked List

• Link − Each Link of a linked list can store a data called an element.
• Next − Each Link of a linked list contain a link to next link called Next.
• Prev − Each Link of a linked list contain a link to previous link called Prev.
• LinkedList − A LinkedList contains the connection link to the first Link called First and to the last link called Last.

Doubly Linked List Representation

As per above shown illustration, following are the important points to be considered.

• Doubly LinkedList contains an link element called first and last.
• Each Link carries a data field(s) and a Link Field called next.
• Each Link is linked with its next link using its next link.
• Each Link is linked with its previous link using its prev link.
• Last Link carries a Link as null to mark the end of the list.

Basic Operations

Following are the basic operations supported by an list.

• Insertion − add an element at the beginning of the list.
• Deletion − delete an element at the beginning of the list.
• Insert Last − add an element in the end of the list.
• Delete Last − delete an element from the end of the list.
• Insert After − add an element after an item of the list.
• Delete − delete an element from the list using key.
• Display forward − displaying complete list in forward manner.
• Display backward − displaying complete list in backward manner.

Insertion Operation

Following code demonstrate insertion operation at beginning in a doubly linked list.

//insert link at the first location
void insertFirst(int key, int data) {

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
 
   if(isEmpty()) {
      //make it the last link
      last = link;
   }else {
      //update first prev link
      head->prev = link;
   }

   //point it to old first link
   link->next = head;
 
   //point first to new first link
   head = link;
}

Deletion Operation

Following code demonstrate deletion operation at beginning in a doubly linked list.

//delete first item
struct node* deleteFirst() {

   //save reference to first link
   struct node *tempLink = head;
 
   //if only one link
   if(head->next == NULL) {
      last = NULL;
   }else {
      head->next->prev = NULL;
   }
 
   head = head->next;
 
   //return the deleted link
   return tempLink;
}

Insertion at End Operation

Following code demonstrate insertion operation at last position in a doubly linked list.

//insert link at the last location
void insertLast(int key, int data) {

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
 
   if(isEmpty()) {
      //make it the last link
      last = link;
   }else {
      //make link a new last link
      last->next = link;     
      //mark old last node as prev of new link
      link->prev = last;
   }

   //point last to new last node
   last = link;
}

Doubly Linked List is a variation of Linked list in which navigation is possible in both ways either forward and backward easily as compared to Single Linked List.

Implementation in C

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>

struct node {
   int data;
   int key;
 
   struct node *next;
   struct node *prev;
};

//this link always point to first Link 
struct node *head = NULL;

//this link always point to last Link 
struct node *last = NULL;

struct node *current = NULL;

//is list empty
bool isEmpty(){
   return head == NULL;
}

int length(){
   int length = 0;
   struct node *current;
 
   for(current = head; current != NULL; current = current->next){
      length++;
   }
 
   return length;
}

//display the list in from first to last
void displayForward(){

   //start from the beginning
   struct node *ptr = head;
 
   //navigate till the end of the list
   printf("\n[ ");
 
   while(ptr != NULL){        
      printf("(%d,%d) ",ptr->key,ptr->data);
      ptr = ptr->next;
   }
 
   printf(" ]");
}

//display the list from last to first
void displayBackward(){

   //start from the last
   struct node *ptr = last;
 
   //navigate till the start of the list
   printf("\n[ ");
 
   while(ptr != NULL){    
 
      //print data
      printf("(%d,%d) ",ptr->key,ptr->data);
  
      //move to next item
      ptr = ptr ->prev;
      printf(" ");
   }
 
   printf(" ]");
}


//insert link at the first location
void insertFirst(int key, int data){

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
 
   if(isEmpty()){
      //make it the last link
      last = link;
   }else {
      //update first prev link
      head->prev = link;
   }

   //point it to old first link
   link->next = head;
 
   //point first to new first link
   head = link;
}

//insert link at the last location
void insertLast(int key, int data){

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
 
   if(isEmpty()){
      //make it the last link
      last = link;
   }else {
      //make link a new last link
      last->next = link;     
      //mark old last node as prev of new link
      link->prev = last;
   }

   //point last to new last node
   last = link;
}

//delete first item
struct node* deleteFirst(){

   //save reference to first link
   struct node *tempLink = head;
 
   //if only one link
   if(head->next == NULL){
      last = NULL;
   }else {
      head->next->prev = NULL;
   }
 
   head = head->next;
   //return the deleted link
   return tempLink;
}

//delete link at the last location

struct node* deleteLast(){
   //save reference to last link
   struct node *tempLink = last;
 
   //if only one link
   if(head->next == NULL){
      head = NULL;
   }else {
      last->prev->next = NULL;
   }
 
   last = last->prev;
 
   //return the deleted link
   return tempLink;
}

//delete a link with given key

struct node* delete(int key){

   //start from the first link
   struct node* current = head;
   struct node* previous = NULL;
 
   //if list is empty
   if(head == NULL){
      return NULL;
   }

   //navigate through list
   while(current->key != key){
      //if it is last node
  
      if(current->next == NULL){
         return NULL;
      }else {
         //store reference to current link
         previous = current;
   
         //move to next link
         current = current->next;             
      }
   }

   //found a match, update the link
   if(current == head) {
      //change first to point to next link
      head = head->next;
   }else {
      //bypass the current link
      current->prev->next = current->next;
   }    

   if(current == last){
      //change last to point to prev link
      last = current->prev;
   }else {
      current->next->prev = current->prev;
   }
 
   return current;
}

bool insertAfter(int key, int newKey, int data){
   //start from the first link
   struct node *current = head; 
 
   //if list is empty
   if(head == NULL){
      return false;
   }

   //navigate through list
   while(current->key != key){
 
      //if it is last node
      if(current->next == NULL){
         return false;
      }else {           
         //move to next link
         current = current->next;             
      }
   }
 
   //create a link
   struct node *newLink = (struct node*) malloc(sizeof(struct node));
   newLink->key = key;
   newLink->data = data;

   if(current == last) {
      newLink->next = NULL; 
      last = newLink; 
   }else {
      newLink->next = current->next;         
      current->next->prev = newLink;
   }
 
   newLink->prev = current; 
   current->next = newLink; 
   return true; 
}

main() {

   insertFirst(1,10);
   insertFirst(2,20);
   insertFirst(3,30);
   insertFirst(4,1);
   insertFirst(5,40);
   insertFirst(6,56); 

   printf("\nList (First to Last): ");  
   displayForward();
 
   printf("\n");
   printf("\nList (Last to first): "); 
   displayBackward();

   printf("\nList , after deleting first record: ");
   deleteFirst();        
   displayForward();

   printf("\nList , after deleting last record: ");  
   deleteLast();
   displayForward();

   printf("\nList , insert after key(4) : ");  
   insertAfter(4,7, 13);
   displayForward();

   printf("\nList  , after delete key(4) : ");  
   delete(4);
   displayForward();
}

If we compile and run the above program then it would produce following result −

Output

List (First to Last): 
[ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ]

List (Last to first): 
[ (1,10) (2,20) (3,30) (4,1) (5,40) (6,56) ]
List , after deleting first record: 
[ (5,40) (4,1) (3,30) (2,20) (1,10) ]
List , after deleting last record: 
[ (5,40) (4,1) (3,30) (2,20) ]
List , insert after key(4) : 
[ (5,40) (4,1) (4,13) (3,30) (2,20) ]
List , after delete key(4) : 
[ (5,40) (4,13) (3,30) (2,20) ]

Circular Linked List

Circular Linked List is a variation of Linked list in which first element points to last element and last element points to first element. Both Singly Linked List and Doubly Linked List can be made into as circular linked list.

Singly Linked List as Circular

In singly linked list, the next pointer of the last node points to the first node.

Doubly Linked List as Circular

In doubly linked list, the next pointer of the last node points to the first node and the previous pointer of the first node points to the last node making the circular in both directions.

As per above shown illustrations, following are the important points to be considered.

• Last Link's next points to first link of the list in both cases of singly as well as doubly linked list.
• First Link's prev points to the last of the list in case of doubly linked list.

Basic Operations

Following are the important operations supported by a circular list.

• insert − insert an element in the start of the list.
• delete − insert an element from the start of the list.
• display − display the list.

Insertion Operation

Following code demonstrate insertion operation at in a circular linked list based on single linked list.

//insert link at the first location
void insertFirst(int key, int data) {
   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data= data;
 
   if (isEmpty()) {
      head = link;
      head->next = head;
   }else {
      //point it to old first node
      link->next = head;
  
      //point first to new first node
      head = link;
   }   
   
}

Deletion Operation

Following code demonstrate deletion operation at in a circular linked list based on single linked list.

//delete first item
struct node * deleteFirst() {
   //save reference to first link
   struct node *tempLink = head;
 
   if(head->next == head){  
      head = NULL;
      return tempLink;
   }     

   //mark next to first link as first 
   head = head->next;
 
   //return the deleted link
   return tempLink;
}

Display List Operation

Following code demonstrate display list operation in a circular linked list.

//display the list
void printList() {
   struct node *ptr = head;
   printf("\n[ ");
 
   //start from the beginning
   if(head != NULL) {
      while(ptr->next != ptr) {     
         printf("(%d,%d) ",ptr->key,ptr->data);
         ptr = ptr->next;
      }
   }
 
   printf(" ]");
}

Implementation in C

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>

struct node {
   int data;
   int key;
 
   struct node *next;
};

struct node *head = NULL;
struct node *current = NULL;

bool isEmpty(){
   return head == NULL;
}

int length(){
   int length = 0;

   //if list is empty
   if(head == NULL){
      return 0;
   }

   current = head->next;

   while(current != head){
      length++;
      current = current->next;   
   }
 
   return length;
}

//insert link at the first location
void insertFirst(int key, int data){

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
 
   if (isEmpty()) {
      head = link;
      head->next = head;
   }else {
      //point it to old first node
      link->next = head;
  
      //point first to new first node
      head = link;
   }    
 
}

//delete first item
struct node * deleteFirst(){

   //save reference to first link
   struct node *tempLink = head;
 
   if(head->next == head){  
      head = NULL;
      return tempLink;
   }     

   //mark next to first link as first 
   head = head->next;
 
   //return the deleted link
   return tempLink;
}

//display the list
void printList(){

   struct node *ptr = head;
   printf("\n[ ");
 
   //start from the beginning
   if(head != NULL){
 
      while(ptr->next != ptr){     
         printf("(%d,%d) ",ptr->key,ptr->data);
         ptr = ptr->next;
      }
  
   }
 
   printf(" ]");
}

main() {

   insertFirst(1,10);
   insertFirst(2,20);
   insertFirst(3,30);
   insertFirst(4,1);
   insertFirst(5,40);
   insertFirst(6,56); 

   printf("Original List: "); 
 
   //print list
   printList();

   while(!isEmpty()){            
      struct node *temp = deleteFirst();
      printf("\nDeleted value:");  
      printf("(%d,%d) ",temp->key,temp->data);        
   }   
 
   printf("\nList after deleting all items: ");          
   printList();   
}

If we compile and run the above program then it would produce following result −

Output

Original List: 
[ (6,56) (5,40) (4,1) (3,30) (2,20) ]
Deleted value:(6,56) 
Deleted value:(5,40) 
Deleted value:(4,1) 
Deleted value:(3,30) 
Deleted value:(2,20) 
Deleted value:(1,10) 
List after deleting all items: 
[ ]

Stack & Queue

1.Stack

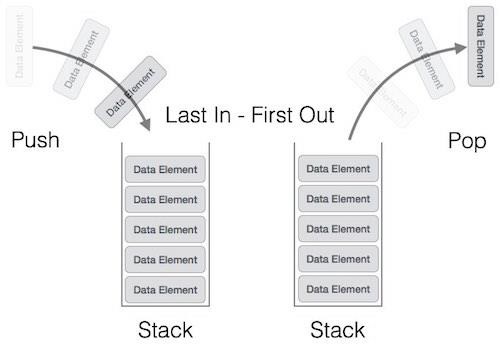
A stack is an abstract data type (ADT), commonly used in most programming languages. It is named stack as it behaves like a real-world stack, for example − deck of cards or pile of plates etc.

A real-world stack allows operations at one end only. For example, we can place or remove a card or plate from top of the stack only. Likewise, Stack ADT allows all data operations at one end only. At any given time, We can only access the top element of a stack.

This feature makes it LIFO data structure. LIFO stands for Last-in-first-out. Here, the element which is placed (inserted or added) last, is accessed first. In stack terminology, insertion operation is called PUSH operation and removal operation is called POP operation.

Stack Representation

Below given diagram tries to depict a stack and its operations −

A stack can be implemented by means of Array, Structure, Pointer and Linked-List. Stack can either be a fixed size one or it may have a sense of dynamic resizing. Here, we are going to implement stack using arrays which makes it a fixed size stack implementation.

Basic Operations

Stack operations may involve initializing the stack, using it and then de-initializing it. Apart from these basic stuffs, a stack is used for the following two primary operations −

• push() − pushing (storing) an element on the stack.
• pop() − removing (accessing) an element from the stack.

When data is PUSHed onto stack.

To use a stack efficiently we need to check status of stack as well. For the same purpose, the following functionality is added to stacks −

• peek() − get the top data element of the stack, without removing it.
• isFull() − check if stack is full.
• isEmpty() − check if stack is empty.

At all times, we maintain a pointer to the last PUSHed data on the stack. As this pointer always represents the top of the stack, hence named top. The toppointer provides top value of the stack without actually removing it.

First we should learn about procedures to support stack functions −

peek()

Algorithm of peek() function −

begin procedure peek

   return stack[top]
   
end procedure

Implementation of peek() function in C programming language −

int peek() {
   return stack[top];
}

isfull()

Algorithm of isfull() function −

begin procedure isfull

   if top equals to MAXSIZE
      return true
   else
      return false
   endif
   
end procedure

Implementation of isfull() function in C programming language −

bool isfull() {
   if(top == MAXSIZE)
      return true;
   else
      return false;
}

isempty()

Algorithm of isempty() function −

begin procedure isempty

   if top less than 1
      return true
   else
      return false
   endif
   
end procedure

Implementation of isempty() function in C programming language is slightly different. We initialize top at -1, as index in array starts from 0. So we check if top is below zero or -1 to determine if stack is empty. Here's the code −

bool isempty() {
   if(top == -1)
      return true;
   else
      return false;
}

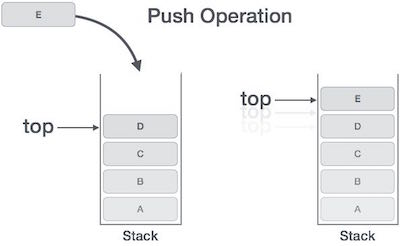
PUSH Operation

The process of putting a new data element onto stack is known as PUSHOperation. Push operation involves series of steps −

• Step 1 − Check if stack is full.
• Step 2 − If stack is full, produce error and exit.
• Step 3 − If stack is not full, increment top to point next empty space.
• Step 4 − Add data element to the stack location, where top is pointing.
• Step 5 − return success.

if linked-list is used to implement stack, then in step 3, we need to allocate space dynamically.

Algorithm for PUSH operation

A simple algorithm for Push operation can be derived as follows −

begin procedure push: stack, data

   if stack is full
      return null
   endif
   
   top ← top + 1
   
   stack[top] ← data

end procedure

Implementation of this algorithm in C, is very easy. See the below code −

void push(int data) {
   if(!isFull()) {
      top = top + 1;   
      stack[top] = data;
   }else {
      printf("Could not insert data, Stack is full.\n");
   }
}

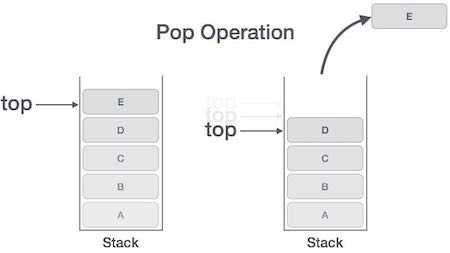
Pop Operation

Accessing the content while removing it from stack, is known as pop operation. In array implementation of pop() operation, data element is not actually removed, instead top is decremented to a lower position in stack to point to next value. But in linked-list implementation, pop() actually removes data element and deallocates memory space.

A POP operation may involve the following steps −

• Step 1 − Check if stack is empty.
• Step 2 − If stack is empty, produce error and exit.
• Step 3 − If stack is not empty, access the data element at which top is pointing.
• Step 4 − Decrease the value of top by 1.
• Step 5 − return success.

Algorithm for POP operation

A simple algorithm for Pop operation can be derived as follows −

begin procedure pop: stack

   if stack is empty
      return null
   endif
   
   data ← stack[top]
   
   top ← top - 1
   
   return data

end procedure

Implementation of this algorithm in C, is shown below −

int pop(int data) {

   if(!isempty()) {
      data = stack[top];
      top = top - 1;   
      return data;
   }else {
      printf("Could not retrieve data, Stack is empty.\n");
   }
}

Queue

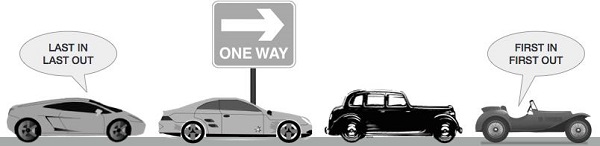
Queue is an abstract data structure, somewhat similar to Stack. In contrast to Queue, queue is opened at both end. One end is always used to insert data (enqueue) and the other is used to remove data (dequeue). Queue follows First-In-First-Out methodology, i.e., the data item stored first will be accessed first.

A real world example of queue can be a single-lane one-way road, where the vehicle enters first, exits first. More real-world example can be seen as queues at ticket windows & bus-stops.

Queue Representation

As we now understand that in queue, we access both ends for different reasons, a diagram given below tries to explain queue representation as data structure −

Same as Queue, queue can also be implemented using Array, Linked-list, Pointer and Structures. For the sake of simplicity we shall implement queue using one-dimensional array.

Basic Operations

Queue operations may involve initializing or defining the queue, utilizing it and then completing erasing it from memory. Here we shall try to understand basic operations associated with queues −

• enqueue() − add (store) an item to the queue.
• dequeue() − remove (access) an item from the queue.

Few more functions are required to make above mentioned queue operation efficient. These are −

• peek() − get the element at front of the queue without removing it.
• isfull() − checks if queue is full.
• isempty() − checks if queue is empty.

In queue, we always dequeue (or access) data, pointed by front pointer and while enqueing (or storing) data in queue we take help of rear pointer.

Let's first learn about supportive functions of a queue −

peek()

Like Queues, this function helps to see the data at the front of the queue. Algorithm of peek() function −

begin procedure peek

   return queue[front]
   
end procedure

Implementation of peek() function in C programming language −

int peek() {
   return queue[front];
}

isfull()

As we are using single dimension array to implement queue, we just check for the rear pointer to reach at MAXSIZE to determine that queue is full. In case we maintain queue in a circular linked-list, the algorithm will differ. Algorithm of isfull() function −

begin procedure isfull

   if rear equals to MAXSIZE
      return true
   else
      return false
   endif
   
end procedure

Implementation of isfull() function in C programming language −

bool isfull() {
   if(rear == MAXSIZE - 1)
      return true;
   else
      return false;
}

isempty()

Algorithm of isempty() function −

begin procedure isempty

   if front is less than MIN  OR front is greater than rear
      return true
   else
      return false
   endif
   
end procedure

If value of front is less than MIN or 0, it tells that queue is not yet initialized, hence empty.

Here's the C programming code −

bool isempty() {
   if(front < 0 || front > rear) 
      return true;
   else
      return false;
}

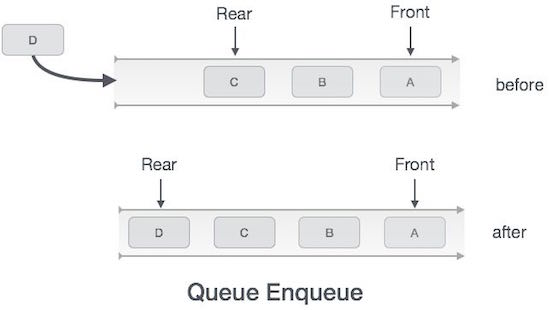
Enqueue Operation

As queue maintains two data pointers, front and rear, its operations are comparatively more difficult to implement than Queue.

The following steps should be taken to enqueue (insert) data into a queue −

• Step 1 − Check if queue is full.
• Step 2 − If queue is full, produce overflow error and exit.
• Step 3 − If queue is not full, increment rear pointer to point next empty space.
• Step 4 − Add data element to the queue location, where rear is pointing.
• Step 5 − return success.

Sometimes, we also check that if queue is initialized or not to handle any unforeseen situations.

Algorithm for enqueue operation

procedure enqueue(data)      
   if queue is full
      return overflow
   endif
   
   rear ← rear + 1
   
   queue[rear] ← data
   
   return true
   
end procedure

Implementation of enqueue() in C programming language −

int enqueue(int data)      
   if(isfull())
      return 0;
   
   rear = rear + 1;
   queue[rear] = data;
   
   return 1;
end procedure

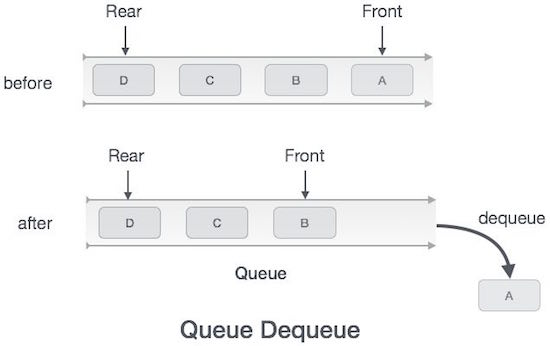
Dequeue Operation

Accessing data from queue is a process of two tasks − access the data wherefront is pointing and remove the data after access. The following steps are taken to perform dequeue operation −

• Step 1 − Check if queue is empty.
• Step 2 − If queue is empty, produce underflow error and exit.
• Step 3 − If queue is not empty, access data where front is pointing.
• Step 3 − Increment front pointer to point next available data element.
• Step 5 − return success.

Algorithm for dequeue operation −

procedure dequeue
   if queue is empty
      return underflow
   end if

   data = queue[front]
   front ← front + 1
   
   return true
end procedure

Implementation of dequeue() in C programming language −

int dequeue() {

   if(isempty())
      return 0;

   int data = queue[front];
   front = front + 1;

   return data;
}

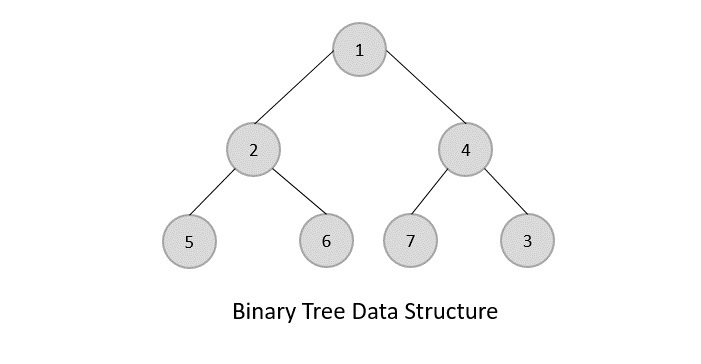
Tree Data Structure - 

Tree represents nodes connected by edges. We'll going to discuss binary tree or binary search tree specifically.

Binary Tree is a special datastructure used for data storage purposes. A binary tree has a special condition that each node can have two children at maximum. A binary tree have benefits of both an ordered array and a linked list as search is as quick as in sorted array and insertion or deletion operation are as fast as in linked list.

Terms

Following are important terms with respect to tree.

• Path − Path refers to sequence of nodes along the edges of a tree.
• Root − Node at the top of the tree is called root. There is only one root per tree and one path from root node to any node.
• Parent − Any node except root node has one edge upward to a node called parent.
• Child − Node below a given node connected by its edge downward is called its child node.
• Leaf − Node which does not have any child node is called leaf node.
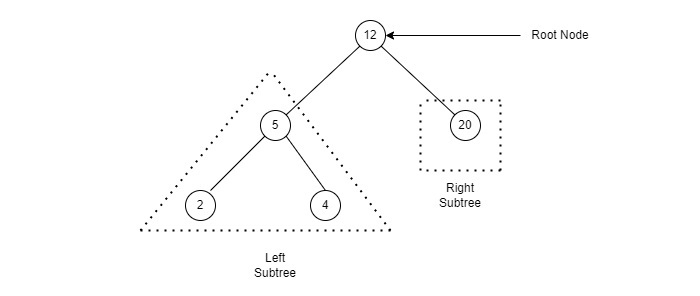
• Subtree − Subtree represents descendents of a node.
• Visiting − Visiting refers to checking value of a node when control is on the node.
• Traversing − Traversing means passing through nodes in a specific order.
• Levels − Level of a node represents the generation of a node. If root node is at level 0, then its next child node is at level 1, its grandchild is at level 2 and so on.
• keys − Key represents a value of a node based on which a search operation is to be carried out for a node.

Binary Search Tree Representation

Binary Search tree exhibits a special behaviour. A node's left child must have value less than its parent's value and node's right child must have value greater than it's parent value.

We're going to implement tree using node object and connecting them through references.

Node

A tree node should look like the below structure. It has data part and references to its left and right child nodes.

struct node {
   int data;   
   struct node *leftChild;
   struct node *rightChild;
};

In a tree, all nodes share common construct.

BST Basic Operations

The basic operations that can be performed on binary search tree data structure, are following −

• Insert − insert an element in a tree / create a tree.
• Search − search an element in a tree.
• Preorder Traversal − traverse a tree in a preorder manner.
• Inorder Traversal − traverse a tree in an inorder manner.
• Postorder Traversal − traverse a tree in a postorder manner.

We shall learn creating (inserting into) tree structure and searching a data-item in a tree in this chapter. We shall learn about tree traversing methods in the coming one.

Insert Operation

The very first insertion creates the tree. Afterwards, whenever an element is to be inserted. First locate its proper location. Start search from root node then if data is less than key value, search empty location in left subtree and insert the data. Otherwise search empty location in right subtree and insert the data.

Algorithm

If root is NULL 
   then create root node
return

If root exists then
   compare the data with node.data
   
   while until insertion position is located

      If data is greater than node.data
         goto right subtree
      else
         goto left subtree

   endwhile 
   
   insert data
 
end If      

Implementation

The implementation of insert function should look like this −

void insert(int data) {
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;

   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty, create root node
   if(root == NULL) {
      root = tempNode;
   }else {
      current = root;
      parent  = NULL;

      while(1) {                
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;                
            
            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }
   
         //go to right of the tree
         else {
            current = current->rightChild;
            
            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }            
   }
}

Search Operation

Whenever an element is to be search. Start search from root node then if data is less than key value, search element in left subtree otherwise search element in right subtree. Follow the same algorithm for each node.

Algorithm

If root.data is equal to search.data
   return root
else
   while data not found

      If data is greater than node.data
         goto right subtree
      else
         goto left subtree
         
      If data found
         return node

   endwhile 
   
   return data not found
   
end if      

The implementation of this algorithm should look like this.

struct node* search(int data) {
   struct node *current = root;
   printf("Visiting elements: ");

   while(current->data != data) {
      if(current != NULL)
      printf("%d ",current->data); 
      
      //go to left tree

      if(current->data > data) {
         current = current->leftChild;
      }
      //else go to right tree
      else {                
         current = current->rightChild;
      }

      //not found
      if(current == NULL) {
         return NULL;
      }

      return current;
   }  
}

Data Structure - Tree Traversal

Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot random access a node in tree. There are three ways which we use to traverse a tree −

• In-order Traversal
• Pre-order Traversal
• Post-order Traversal

Generally we traverse a tree to search or locate given item or key in the tree or to print all the values it contains.

Inorder Traversal

In this traversal method, the left left-subtree is visited first, then root and then the right sub-tree. We should always remember that every node may represent a subtree itself.

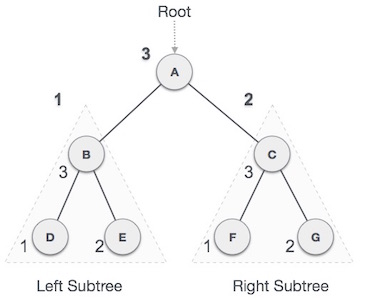
If a binary tree is traversed inorder, the output will produce sorted key values in ascending order.

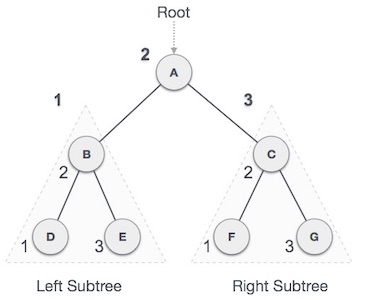
We start from A, and following in-order traversal, we move to its left subtree B.B is also traversed in-ordered. And the process goes on until all the nodes are visited. The output of in-order traversal of this tree will be −

D → B → E → A → F → C → G

Algorithm

Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Visit root node.
Step 3 − Recursively traverse right subtree.

Preorder Traversal

In this traversal method, the root node is visited first, then left subtree and finally right sub-tree.

We start from A, and following pre-order traversal, we first visit A itself and then move to its left subtree B. B is also traversed pre-ordered. And the process goes on until all the nodes are visited. The output of pre-order traversal of this tree will be −

A → B → D → E → C → F → G

Algorithm

Until all nodes are traversed −
Step 1 − Visit root node.
Step 2 − Recursively traverse left subtree.
Step 3 − Recursively traverse right subtree.

Postorder Traversal

In this traversal method, the root node is visited last, hence the name. First we traverse left subtree, then right subtree and finally root.

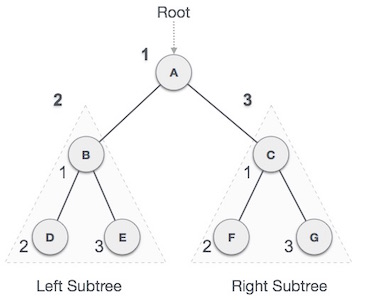
We start from A, and following pre-order traversal, we first visit left subtree B.B is also traversed post-ordered. And the process goes on until all the nodes are visited. The output of post-order traversal of this tree will be −

D → E → B → F → G → C → A

Algorithm

Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Recursively traverse right subtree.
Step 3 − Visit root node.

Binary Search Tree

A binary search tree (BST) is a tree in which all nodes follows the below mentioned properties −

• The left sub-tree of a node has key less than or equal to its parent node's key.
• The right sub-tree of a node has key greater than or equal to its parent node's key.

Thus, a binary search tree (BST) divides all its sub-trees into two segments;left sub-tree and right sub-tree and can be defined as −

left_subtree (keys)  ≤  node (key)  ≤  right_subtree (keys)

Representation

BST is a collection of nodes arranged in a way where they maintain BST properties. Each node has key and associated value. While searching, the desired key is compared to the keys in BST and if found, the associated value is retrieved.

An example of BST −

We observe that the root node key (27) has all less-valued keys on the left sub-tree and higher valued keys on the right sub-tree.

Basic Operations

Following are basic primary operations of a tree which are following.

• Search − search an element in a tree.
• Insert − insert an element in a tree.
• Preorder Traversal − traverse a tree in a preorder manner.
• Inorder Traversal − traverse a tree in an inorder manner.
• Postorder Traversal − traverse a tree in a postorder manner.

Node

Define a node having some data, references to its left and right child nodes.

struct node {
   int data;   
   struct node *leftChild;
   struct node *rightChild;
};

Search Operation

Whenever an element is to be search. Start search from root node then if data is less than key value, search element in left subtree otherwise search element in right subtree. Follow the same algorithm for each node.

struct node* search(int data){
   struct node *current = root;
   printf("Visiting elements: ");
 
   while(current->data != data){
 
      if(current != NULL) {
         printf("%d ",current->data);
   
         //go to left tree
         if(current->data > data){
            current = current->leftChild;
         }//else go to right tree
         else {                
            current = current->rightChild;
         }
   
         //not found
         if(current == NULL){
            return NULL;
         }
      }   
   }
   return current;
}

Insert Operation

Whenever an element is to be inserted. First locate its proper location. Start search from root node then if data is less than key value, search empty location in left subtree and insert the data. Otherwise search empty location in right subtree and insert the data.

void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;

   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL){
      root = tempNode;
   }else {
      current = root;
      parent = NULL;

      while(1){                
         parent = current;
   
         //go to left of the tree
         if(data < parent->data){
            current = current->leftChild;                
            //insert to the left
    
            if(current == NULL){
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else{
            current = current->rightChild;
            //insert to the right
            if(current == NULL){
               parent->rightChild = tempNode;
               return;
            }
         }
      }            
   }
}        

---

Huffman algorithm

What is the Huffman algorithm?

- In Huffman Algorithm, a set of nodes assigned with values is fed to the algorithm.

- Initially 2 nodes are considered and their sum forms their parent node. 

- When a new element is considered, it can be added to the tree. 

- Its value and the previously calculated sum of the tree are used to form the new node which in turn becomes their parent.

- This algorithm is based on the frequency of occurrence of a data item.

- It uses a specific method for choosing the representation for each symbol.

Operation of the Huffman algorithm

Initial data sorted by frequency
	Combine the two lowest frequencies, F and E, to form a sub-tree of weight 14.Move it into its correct place.
	Again combine the two lowest frequencies, C and B, to form a sub-tree of weight 25.Move it into its correct place.
	Now the sub-tree with weight, 14, and D are combined to make a tree of weight, 30.Move it to its correct place.
	Now the two lowest weights are held by the "25" and "30" sub-trees, so combine them to make one of weight, 55.Move it after the A.
	Finally, combine the A and the "55" sub-tree to produce the final tree.The encoding table is: A 0 C 100 B 101 F 1100 E 1101 D 111

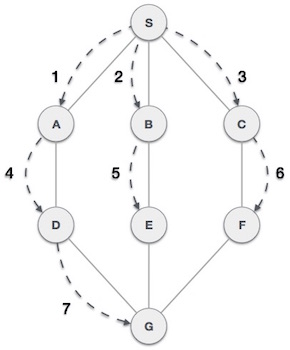
Graph Data Structure

A graph is a pictorial representation of a set of objects where some pairs of objects are connected by links. The interconnected objects are represented by points termed as vertices, and the links that connect the vertices are callededges.

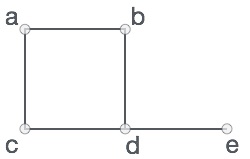
Formally, a graph is a pair of sets (V, E), where V is the set of vertices and E is the set of edges, connecting the pairs of vertices. Take a look at the following graph −

In the above graph,

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

Graph Data Structure

Mathematical graphs can be represented in data-structure. We can represent a graph using an array of vertices and a two dimensional array of edges. Before we proceed further, let's familiarize ourselves with some important terms −

• Vertex − Each node of the graph is represented as a vertex. In example given below, labeled circle represents vertices. So A to G are vertices. We can represent them using an array as shown in image below. Here A can be identified by index 0. B can be identified using index 1 and so on.
• Edge − Edge represents a path between two vertices or a line between two vertices. In example given below, lines from A to B, B to C and so on represents edges. We can use a two dimensional array to represent array as shown in image below. Here AB can be represented as 1 at row 0, column 1, BC as 1 at row 1, column 2 and so on, keeping other combinations as 0.
• Adjacency − Two node or vertices are adjacent if they are connected to each other through an edge. In example given below, B is adjacent to A, C is adjacent to B and so on.
• Path − Path represents a sequence of edges between two vertices. In example given below, ABCD represents a path from A to D.

Basic Operations

Following are basic primary operations of a Graph which are following.

• Add Vertex − add a vertex to a graph.
• Add Edge − add an edge between two vertices of a graph.
• Display Vertex − display a vertex of a graph.

Traversal in Graphic

Depth First Search algorithm(DFS) traverses a graph in a depthward motion and uses a stack to remember to get the next vertex to start a search when a dead end occurs in any iteration.

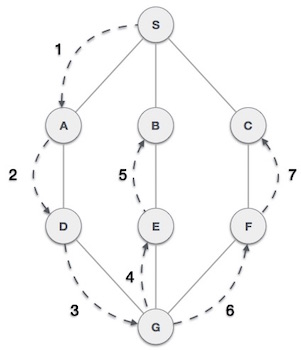
As in example given above, DFS algorithm traverses from A to B to C to D first then to E, then to F and lastly to G. It employs following rules.

• Rule 1 − Visit adjacent unvisited vertex. Mark it visited. Display it. Push it in a stack.
• Rule 2 − If no adjacent vertex found, pop up a vertex from stack. (It will pop up all the vertices from the stack which do not have adjacent vertices.)
• Rule 3 − Repeat Rule 1 and Rule 2 until stack is empty.

Step	Traversal	Description
1.		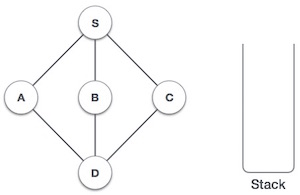Initialize the stack
2.		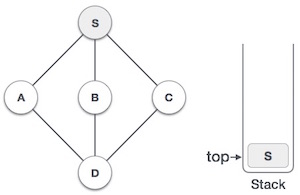Mark S as visited and put it onto the stack. Explore any unvisited adjacent node from S. We have three nodes and we can pick any of them. For this example, we shall take the node in alphabetical order.
3.		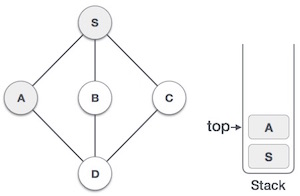Mark A as visited and put it onto the stack. Explore any unvisited adjacent node from A. Both Sand D are adjacent to A but we are concerned for unvisited nodes only.
4.		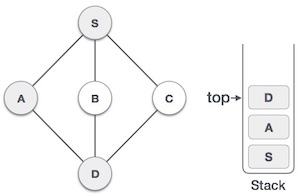Visit D and mark it visited and put onto the stack. Here we have B and C nodes which are adjacent to D and both are unvisited. But we shall again choose in alphabetical order.
5.		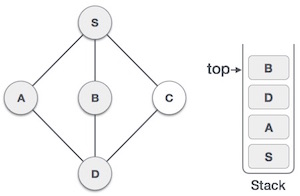We choose B, mark it visited and put onto stack. Here B does not have any unvisited adjacent node. So we pop B from the stack.
6.		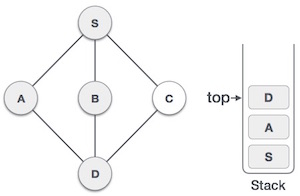We check stack top for return to previous node and check if it has any unvisited nodes. Here, we find D to be on the top of stack.
7.		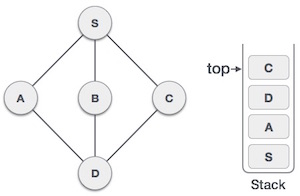Only unvisited adjacent node is from D is C now. So we visit C, mark it visited and put it onto the stack.

As C does not have any unvisited adjacent node so we keep popping the stack until we find a node which has unvisited adjacent node. In this case, there's none and we keep popping until stack is empty.

Breadth First Traversal

Breadth First Search algorithm(BFS) traverses a graph in a breadthwards motion and uses a queue to remember to get the next vertex to start a search when a dead end occurs in any iteration.

As in example given above, BFS algorithm traverses from A to B to E to F first then to C and G lastly to D. It employs following rules.

• Rule 1 − Visit adjacent unvisited vertex. Mark it visited. Display it. Insert it in a queue.
• Rule 2 − If no adjacent vertex found, remove the first vertex from queue.
• Rule 3 − Repeat Rule 1 and Rule 2 until queue is empty.

Step	Traversal	Description
1.		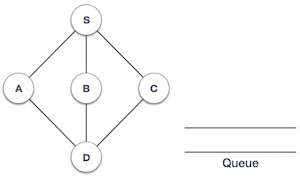Initialize the queue.
2.		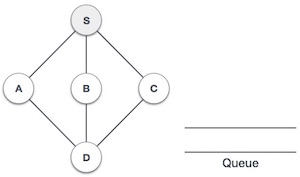We start from visiting S(starting node), and mark it visited.
3.		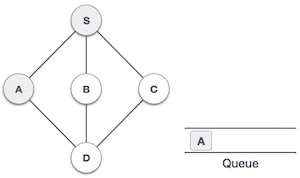We then see unvisited adjacent node from S. In this example, we have three nodes but alphabetically we choose A mark it visited and enqueue it.
4.		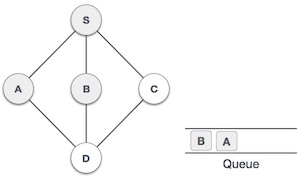Next unvisited adjacent node from S is B. We mark it visited and enqueue it.
5.		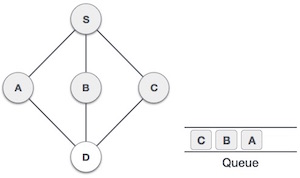Next unvisited adjacent node from S is C. We mark it visited and enqueue it.
6.		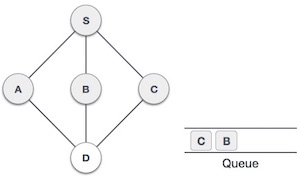Now S is left with no unvisited adjacent nodes. So we dequeue and find A.
7.		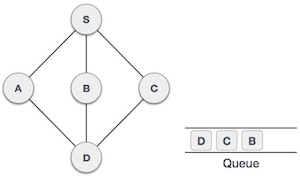From A we have D as unvisited adjacent node. We mark it visited and enqueue it.

At this stage we are left with no unmarked (unvisited) nodes. But as per algorithm we keep on dequeuing in order to get all unvisited nodes. When the queue gets emptied the program is over.